Philips Semiconductors Application note
AN1651Using the NE/SA5234 amplifier
1991 Oct
8
VIII. GAIN-BANDWIDTH VS CLOSED LOOP FRE-
QUENCY RESPONSE
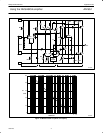
Figure 5 shows the small signal frequency response of the NE5234
versus closed-loop gain in dB. The test circuit is shown in Figure 6.
The plot is taken from measured data and thus shows how each
value of closed-loop gain coincides with the open-loop response
curve. The NE/SA5234’s open-loop gain response has a uniform
6dB/octave roll-off which continues beyond 2.5MHz. This factor
guarantees each op amp in the IC a high stability in virtually any
gain configuration. In making these measurements, dual supplies of
±2.5V were used in order to allow a grounded reference plane and
no coupling capacitors which might cause frequency related errors.
A critical parameter which affects the reproduction quality of
complex waveforms is the gain-bandwidth-product of the operational
amplifier. Essentially, this is a measure of the maximum frequency
handling characteristics of any operational amplifier for a given
closed-loop gain. As is evident from the graph, the NE/SA5234 has
a 2.5MHz unity gain cross-over frequency — much higher than most
other low voltage op amps. For comparison, the µA741 has a
gain-bandwidth-product of 1MHz, as do the LM324 and the
MC3403.
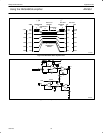
IX. LOOP-GAIN
The dynamic signal response of any closed-loop amplifier stage is a
function of the Loop-gain of that particular stage. Loop-gain is equal
to the open-loop gain in dB, at a given frequency, minus the
closed-loop gain of the stage. The greater the Loop-gain, the lower
the transfer function error of the device. Essentially, any parametric
error is reduced by the factor of the Loop-gain. This includes output
resistance and output signal voltage accuracy. It is good practice
then to maximize Loop-gain to the degree that stage gain may be
sacrificed for bandwidth. In some cases it is actually better to use
two stages of gain in order to preserve signal quality than to use one
high gain stage. Of course, there is a trade-off between the
aforementioned factors that affect the signal-to-noise ratio of the
stage and optimizing the Loop-gain. For example, a voice-band
audio stage which requires 3kHz bandwidth, should be limited to a
closed-loop gain of 40dB for lowest distortion in the output signal.
For higher quality audio applications requiring a 20kHz bandwidth,
the closed-loop gain must be limited to 20dB. This results in a
Loop-gain of 20dB at the highest signal frequency.
A second consideration in the list of frequency dependent
parameters is the effect of amplifier slew rate. Not only is it
frequency dependent but it is also a function of signal amplitude, as
we shall see in the next section.
LOOP
GAIN
A
OL
A
CL
f
S
f
u
-6dB/Octave
SL00640
Figure 12.
X. SLEW RATE RESPONSE
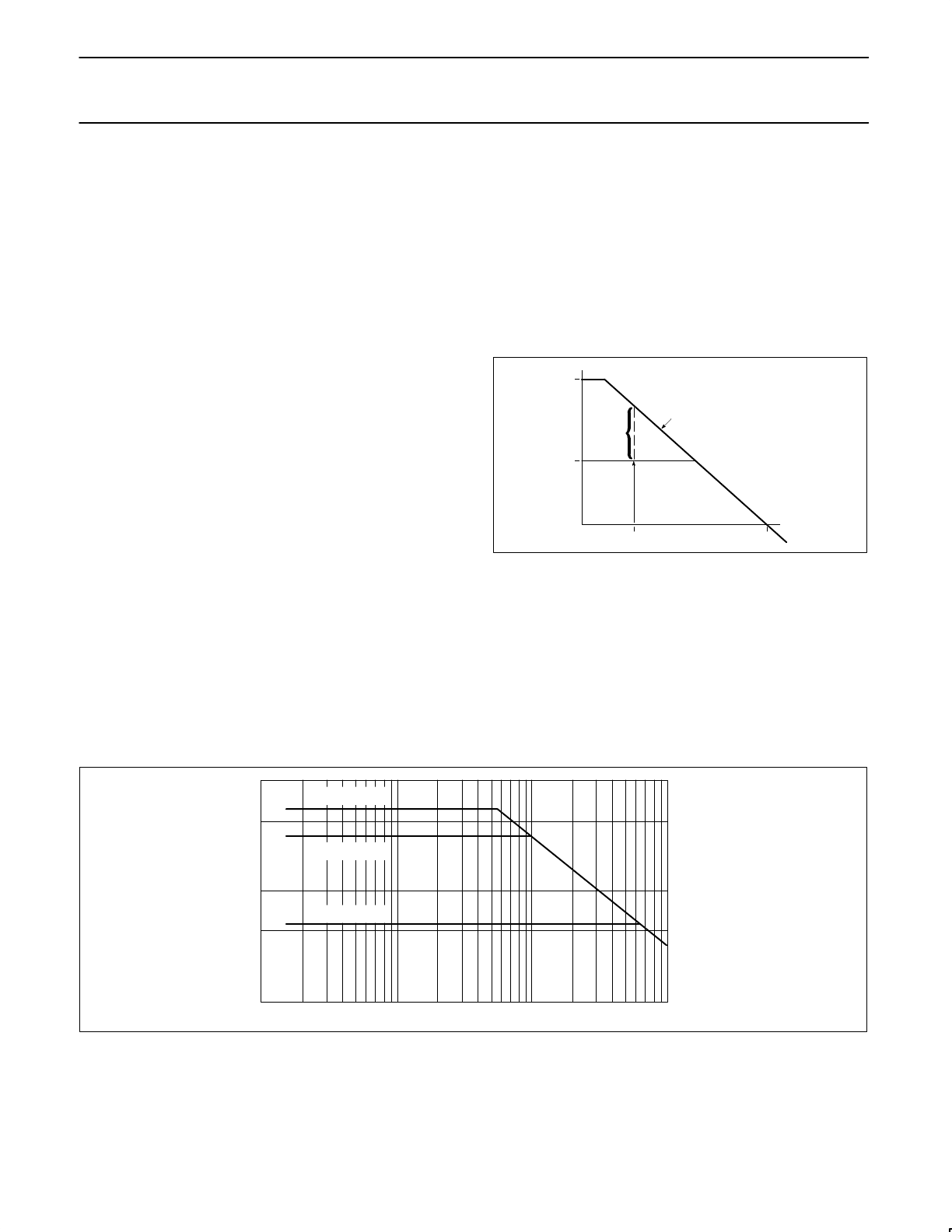
The slew rate of an operational amplifier determines how fast it can
respond to a signal, and is measured in volts-per-microsecond. The
NE5234 has a typical slew rate of 0.8V/µs. Let us see just what this
means in terms of signal handling capability. If a sinusoidal input
signal, V
S
, is used as reference, it is specified by its frequency and
peak amplitude, V
P
as follows:
(EQ. 11.)
V
S
+ V
P
sin (2p f t)
2
VOLTS PK
0.02
2000 2000000
(Hz)
V
PK
= 1.096V
V
PK
= 630mV
V
PK
= 100mV
SL00641
Figure 13. Slew Rate Limiting Amplitude vs Frequency
Slew Rate (SR) is the time-rate-of-change of the signal voltage
during any complete cycle, that is over the range of 0 to 2π. This
amounts to taking the time derivative of the sine wave which results
in multiplying the cosine by the factor ‘2πf’.
An example of the trade off between signal amplitude and frequency
is shown below for the NE5234 slew rate of 0.8V/µs. As shown in
Figure 13, the maximum allowable amplitude signal which can be
reproduced is determined by the slew rate response line which gives
peak output volts versus frequency in Hertz.
Mathematically, slew rate is determined, by the equation below, as
the derivative of the sine wave signal. The resultant slew rate
function changes with both frequency and amplitude.